stoldark ::


	<font face=Arial,Helvetica color=#000000 size=2><p>If you are reading this, your browser does not support the IFRAME HTML tag. You will <b>not</b> be able to view the quotes unless you upgrade your browser. Microsoft's <a href="http://www.microsoft.com/windows/ie/default.asp">website</a> is a good place to start.

If there's a question you've been dying to ask, chances are you won't find an answer here. Despite that, here's some answers to questions directed towards my person..... or something along those lines.

Question: How many spare legs do you have?
Answer: Log₃17.

Question: What does the graph of reaction time vs awesomeness look like?
Answer: Because my graph is awesome, it's going to take you a long time to figure this one out.

Question: What's this I hear about a magical formula of life?
Answer: You must be referring to the 2 + 2 = 4 equation. Another formula which may be derived from that equation is the 2 * 2 = 4 equation.

Question: It says in your info section your phone number is 3. I'm too smart for that... what's your real phone number?
Answer: Well, it looks like you've discovered one of my 'tricks'. My real phone number is HAM.

Question: Is that blue guy in the info section supposed to look like you?
Answer: Of course not, he's supposed to look like my identical twin.

Question: I bet my dad can beat up your dad.
Answer: No, he can't. Although this wasn't a real question, it is important to take the time to realize that sometimes, just sometimes, life isn't real either.

Question: Where can I get those nifty bobble head hockey players?
Answer: For a limited time only, you can purchase them. Otherwise, you can't.

Question: Are you sure you didn't manufacture this FAQ list on your own?
Answer: To answer your question, let us examine why sin²Ų+cos²Ų = 1. Consider the image below.

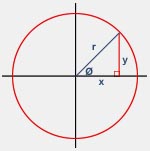
The radial arm, r, of any given length may lie in the red circle as shown. Recalling the principles of trigonometric functions, we can calculate x and y to be equal to rcosŲ and rsinŲ, respectively. Now, since the angle remains constant, the ratios of sides will never change no matter how long the radial arm r is, and the length of x will always lie perpendicular to y. Therefore, the Triangle Trick™ can be used to identify the following relationship:

r² = (rsinŲ)² + (rcosŲ)²
r² = r²sin²Ų + r²cos²Ų
r² = r²(sin²Ų +cos²Ų)
1 = sin²Ų +cos²Ų

Proof is complete, and thus, all is well in the land of mathematics.