|
The applications are widespread, and its significance quite profound, but how often is Pythagoras' Theorem thoroughly contemplated for its simplicity and practicality? My goal here is to provide a quick and dirty geometric proof of our beloved identity.
For the unfamiliar reader, a quick introduction: the following is a proof of the relationship of the two sides opposite the largest side (the hypotenuse) of a right angled triangle (where one angle measures 90°). This relationship is formally known as Pythagoras' Theorem, credited to the mathematician Pythagoras. For our purposes, we will refer to this as the Triangle Trick™.
Indeed. Let us consider the right angled triangle in the following image:
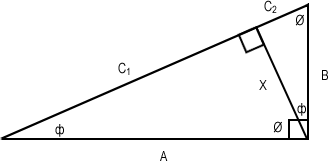The triangle is further divided into two smaller triangles, each of which is also a right angled triangle with similar angle measurements. We identify all three triangles as a similar triangle. For clarification, the additional triangles can be seen in the image below.
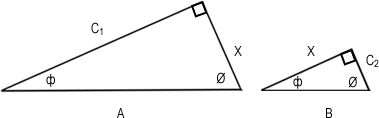A very useful property of similar triangles is that the ratio of sides corresponding to any given angle will be equal among all similar triangles in question. In particular, we see the following relationship:
It will be useful here to define C1 + C2 = C. Isolating for C1 and C2 yields the following expressions:
However, we have defined C1 + C2 = C. Adding these equations and isolating for C we find:
And thus we conclude the derivation of the Triangle Trick™.
Obvious, even. This relationship is none-the- less an important one, because of its incredible usefulness. It is almost trivial to see such a result, and there are, in fact, many ways of deriving this identity.
Until next time kids. Stay alert! Stay safe!
Cheers,
stoldark
[ home | info | portfolio | gallery | contact | links | faq ] ©2002 Diego Benavides
|
