I love math, and I love answering math questions, so this page came in direct response to a thread on this very subject while browsing one of my favorite online forums.



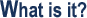
Good question. Just what the hell is the quadratic equation? In a very simplified definition, it's a way of solving for an unknown variable x in an equation. More specifically, an equation where x appears to the power of two, or x2 as the highest power.


Well, if you think of an equation that relates one variable to another in a 2d plane, and you took the time to graph out all the points, you would find that you have a curve on your hands. Sometimes this curve is just a straight line. We're all familiar with our linear equation:

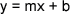So what happens when y is exactly equal to 0 in this equation? We have found the point where this line crosses the x-axis, and we can solve for the value of x explicitly. This is done like so:

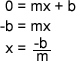Easy enough. But what about when our polynomial equation is taken to the next degree? Namely, consider this example:

y = ax2 + bx + c

Where we know a, b and c are constants which are elements of real numbers.


Please try, really. You need to isolate for x but common factoring won't work in this case. You can pull out the quadratic equation but then you're not really addressing the issue of what the quadratic equation is, are you? Let's try and work through this mathematically. First, you need to be familiar with the concept of completing the square.


Completing the square is a process by which you try to work backwards to get a nice perfect square. A perfect square is any polynomial that can be written in the form:

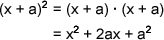Notice the similarities between that expression and the one we're trying to solve? This expression contains an x2 as well but we've got these nasty things in here: a 2a and an a2.

Alright, so now it's time to make our equation, y = ax2 + bx + c, look something closer to a perfect square.


And so the real fun begins. We're going to start by trying to solve for x when y is equal to 0, again, at the x-axis. This leaves us with one less variable to worry about.

0 = ax2 + bx + c

Nicely done. Now we'll divide the whole thing by a so that x2 is all alone and ready to be molested- I mean manipulated.

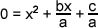Now comes the part where we complete the square. We want to get a form like the one we saw before, where we can factor it into the form (x + a)2. Now it's important to note the a in our equation is not necessarily the a we're going to get in (x + a)2. Just bear with me for a second. What we're going to do is take the value of 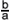, divide it by two, square it, then add it in and subtract it. I know, it sounds odd, but you'll see why in a second.


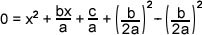
Some of you may be saying "no, you can't do that" or "why the hell did you do that" or "who's your drug dealer, he seems to be doing a great job of keeping you high". To address all your concerns, this is, mathematically correct and possible. Think about it for a second, we've added a term, let's call it m, and subtracted m from the equation as well. It's like adding in 0 to both sides of the equation. Have we changed the original equation at all? No, we've just introduced something to help us out with the problem. Watch closely now.

I've done nothing but re-arrange the equation, but do you see something in regards to the first three terms on the right side of the equals sign? If you look closely, you'll find it's in the form of an expanded perfect square. So it's not in a nice and easy to spot form, but it's there. So now we can factor those terms into a perfect square!

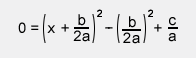Don't believe me? Expand the terms in the first bracket yourself, and you'll find the equation works out to be just like the one in the previous step. What we've accomplished here is isolating x as a term to a degree of 1. We can now solve the rest of this equation through simple arithmetic. I'll explain the steps as I go along, but from here on it it's pretty straight forward.

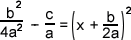Here I expanded the second term in brackets and moved everything not in our perfect square over to the left side of the equation.

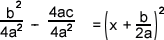In this step I found common denominator for adding the terms on the left.

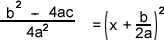And here I just added them.

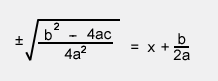In this step I'm now trying to solve for x, but we need to take the square root of both sides first, being careful to remember that the square root of a number can be either positive or negative. Is this starting to look familiar? :)

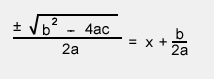Here I've simplified the denominator.

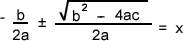A little rearranging and simplification of our equation leads to......

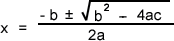Tada! I present, the quadratic equation. So next time you see this in use, stop and admire the functionality it benefits: you don't have to work out all that math just to find out quick and simple what the value(s) of x in an equation are.

At quick glance, you can see there are some restrictions on this formula, namely, the value of a can never be 0. If you look at our original equation you will see this makes sense: y = ax2 + bx + c. If a were 0, then you would have the equation of a straight line and the quadratic forumla need not apply in your solution of x.

Hopefully you have a better understanding of why the quadratic equation is set up the way it is and can walk away with just a little bit more knowledge. Until next time.....

Cheers,
stoldark



[ home | info | portfolio | gallery | contact | links | faq ]

©2002 Diego Benavides